Graph Traversal: A Complete Technical Guide

Graphs are one of the most powerful and widely used data structures in computer science. They help us model and solve real-world problems involving connections, relationships, or networks.

In this blog, we’ll dive deep into:

• What graphs are
• Graph types
• Graph traversal algorithms (DFS & BFS)
• Use cases of graphs and traversals
• Code implementations in Java

---

What is a Graph?

A graph is a collection of nodes (vertices) connected by edges (links). Graphs can represent almost any system with pairwise relationships.

Formal Definition:

A graph G is defined as G = (V, E) where:

• V is a set of vertices.
• E is a set of edges connecting pairs of vertices.

Example:

   A
  / \
 B   C
 |   |
 D---E

Vertices: {A, B, C, D, E}
Edges: {(A, B), (A, C), (B, D), (C, E), (D, E)}

Types of Graphs

Type	Description
Undirected	Edges have no direction (e.g., Facebook friends)
Directed	Edges have direction (e.g., Twitter follows)
Weighted	Edges have weights (e.g., distances on maps)
Unweighted	Edges don’t have weights
Cyclic	Graph contains at least one cycle
Acyclic	No cycles (important for trees, dependency graphs)

Graph Traversal

Graph traversal means visiting every node in a graph in a specific order. It’s the foundation for many graph-related problems.

Main Types of Traversal:

1. Depth-First Search (DFS)
2. Breadth-First Search (BFS)

1. Depth-First Search (DFS)

DFS explores as deep as possible down a path before backtracking.

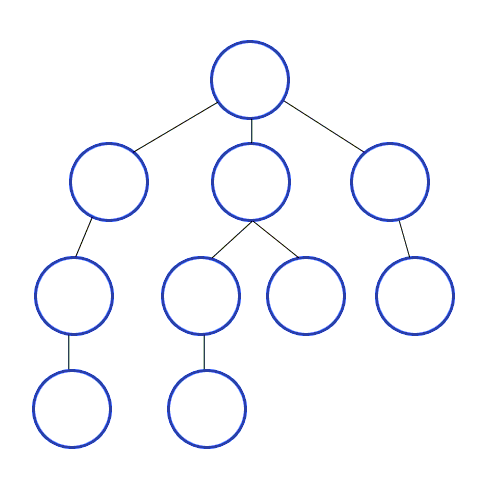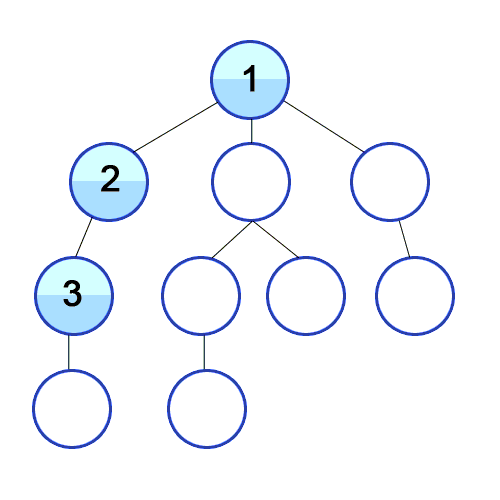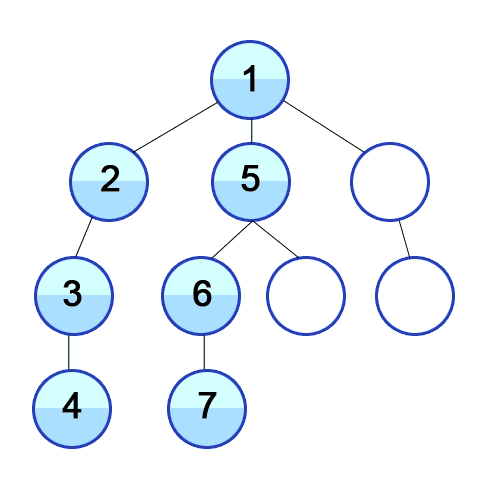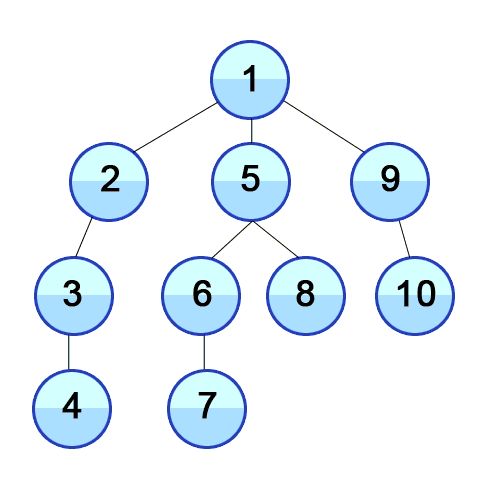
Java Implementation – Recursive:

import java.util.*;

public class DFSRecursive {
    public static void dfs(Map<String, List<String>> graph, String node, Set<String> visited) {
        if (!visited.contains(node)) {
            System.out.print(node + " ");
            visited.add(node);
            for (String neighbor : graph.get(node)) {
                dfs(graph, neighbor, visited);
            }
        }
    }

    public static void main(String[] args) {
        Map<String, List<String>> graph = new HashMap<>();
        graph.put("A", Arrays.asList("B", "C"));
        graph.put("B", Arrays.asList("D"));
        graph.put("C", Arrays.asList("E"));
        graph.put("D", Arrays.asList("E"));
        graph.put("E", new ArrayList<>());

        Set<String> visited = new HashSet<>();
        dfs(graph, "A", visited);  // Output: A B D E C
    }
}

Java Implementation – Iterative:

import java.util.*;

public class DFSIterative {
    public static void dfs(Map<String, List<String>> graph, String start) {
        Set<String> visited = new HashSet<>();
        Stack<String> stack = new Stack<>();
        stack.push(start);

        while (!stack.isEmpty()) {
            String node = stack.pop();
            if (!visited.contains(node)) {
                System.out.print(node + " ");
                visited.add(node);
                List<String> neighbors = graph.get(node);
                for (String neighbor : neighbors) {
                    stack.push(neighbor);
                }
            }
        }
    }

    public static void main(String[] args) {
        Map<String, List<String>> graph = new HashMap<>();
        graph.put("A", Arrays.asList("B", "C"));
        graph.put("B", Arrays.asList("D"));
        graph.put("C", Arrays.asList("E"));
        graph.put("D", Arrays.asList("E"));
        graph.put("E", new ArrayList<>());

        dfs(graph, "A");  // Output: A B D E C
    }
}

2. Breadth-First Search (BFS)

BFS explores the nearest neighbors first, then moves outward.

import java.util.*;

public class BFS {
    public static void bfs(Map<String, List<String>> graph, String start) {
        Set<String> visited = new HashSet<>();
        Queue<String> queue = new LinkedList<>();

        queue.add(start);
        visited.add(start);

        while (!queue.isEmpty()) {
            String node = queue.poll();
            System.out.print(node + " ");
            for (String neighbor : graph.get(node)) {
                if (!visited.contains(neighbor)) {
                    queue.add(neighbor);
                    visited.add(neighbor);
                }
            }
        }
    }

    public static void main(String[] args) {
        Map<String, List<String>> graph = new HashMap<>();
        graph.put("A", Arrays.asList("B", "C"));
        graph.put("B", Arrays.asList("D"));
        graph.put("C", Arrays.asList("E"));
        graph.put("D", Arrays.asList("E"));
        graph.put("E", new ArrayList<>());

        bfs(graph, "A");  // Output: A B C D E
    }
}

Use Cases of Graphs

Domain	Use Case Example
Social Media	Friend recommendations (undirected graph)
Maps & GPS	Finding shortest path (weighted graph)
Web Crawling	Following hyperlinks (directed graph)
Compiler	Dependency resolution (DAG – Directed Acyclic Graph)
Biology	Modeling neural networks, gene networks
Electric Grid	Power flow analysis

Use Cases of Traversals

DFS:

• Topological sorting
• Maze/Pathfinding problems
• Detecting cycles in graphs
• Solving puzzles (like Sudoku)
• Analyzing connected components

BFS:

• Shortest path in unweighted graphs (like Dijkstra without weights)
• Finding levels in trees/graphs
• Crawling/searching data in breadth-first fashion
• Peer-to-peer networks

Time and Space Complexity

Algorithm	Time Complexity	Space Complexity
DFS	O(V + E)	O(V) (call stack/visited)
BFS	O(V + E)	O(V) (queue/visited)

Choosing Between DFS and BFS

Criteria	Choose
You need the shortest path (unweighted)	BFS
You want to search deep paths	DFS
You need to check connectivity	DFS or BFS
You want to find cycle or topological sort	DFS

Advanced Topics (Just to Know)

• Dijkstra’s Algorithm – for shortest path in weighted graphs.
• A* – for optimal pathfinding in games/maps.
• Union-Find (Disjoint Set) – for graph clustering.
• Tarjan’s Algorithm – for strongly connected components (SCCs).
• Bellman-Ford – for graphs with negative weights.

Conclusion

Graph traversal is a foundational concept for solving network-based problems. Whether you’re analyzing social connections, solving mazes, or building search engines, knowing how to use DFS and BFS will make your solutions faster and smarter.

Key Takeaways:

• Graphs model real-world relationships.
• DFS explores deeply, BFS explores broadly.
• Traversal algorithms are essential in pathfinding, analysis, and search.
• Choose your traversal based on problem constraints and goals.

More Algorithms:

Binary Search